Comment coller un double tore?
17 May 2021Bonjour, j’ai décidé d’orienter ce blog-ci vers la vulgarisation et mon blog en anglais vers des thématiques plus proche de ma recherche.
J’avais publié ce billet il y a environ un an en anglais, et il était lié à ma recherche du moment, mais je pense que c’est aussi un joli sujet de vulgarisation. Il s’agit de faire un peu de topologie (algorithmique), avec beaucoup de dessins.
On va parler de topologie dans la veine du fameux «un donut est la même chose qu’une tasse de café : les deux ont un trou». L’idée est de construire un double tore par collage des bords d’un polygone, un peu comme on construit un polytope à partir d’un patron. Mais comme les constructions sont à déformation près, elles ne peuvent pas vraiment être faites en papier, ou alors en papier élastique !
Le double tore est la surface à deux trous. Pour le construire on va partir de l’image suivante qui est appelée « le schéma polygonal du double tore ». C’est un octogone dont les arêtes sont colorées et orientées. Il y a exactement deux arêtes de chaque couleur.
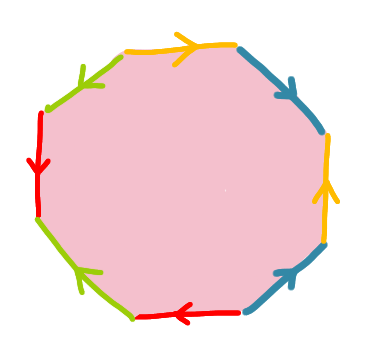
La construction consiste à appliquer l’opération suivante : prendre deux arêtes d’une même couleur, et les coller, tel que les orientations soient cohérentes (les flèches pointent dans le même sens). Commençons avec les arêtes rouges.
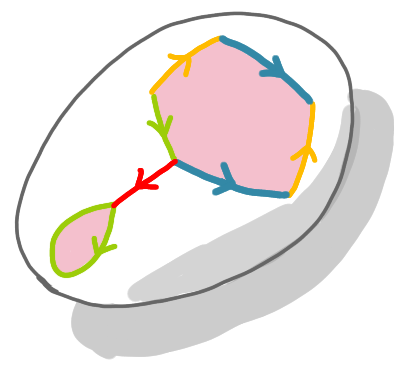
Faisons de même avec les arêtes jaunes.
À ce stade remarquons que comme on va coller toutes les paires d’arêtes, les huit coins du polygone vont devenir le même point. Pour faciliter le dessin, on va coller deux de ces coins pour relier le chemin jaune et le chemin rouge.
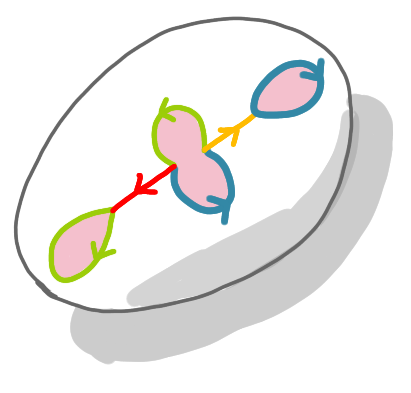
On arrive au cœur de la construction. Nous avons deux boucles vertes. Pour les fusionner, nous allons créer une « poignée », c’est-à-dire une sorte de pont au-dessus de la surface en construction. Cela crée le premier trou. Notez que le chemin rouge devient une boucle.
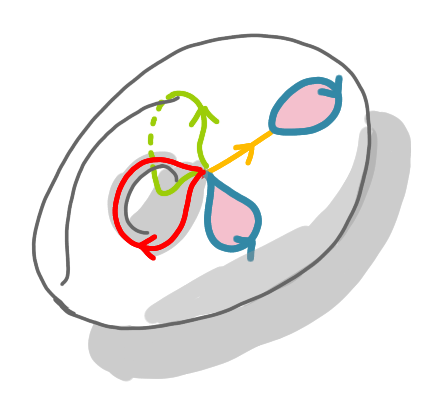
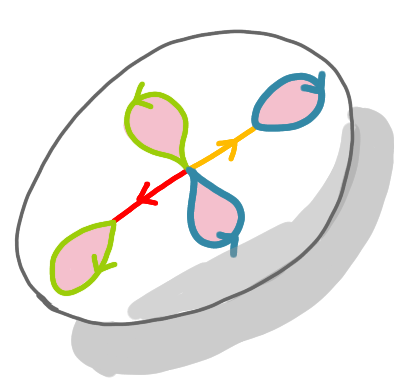
On fait de même avec les boucles bleues.
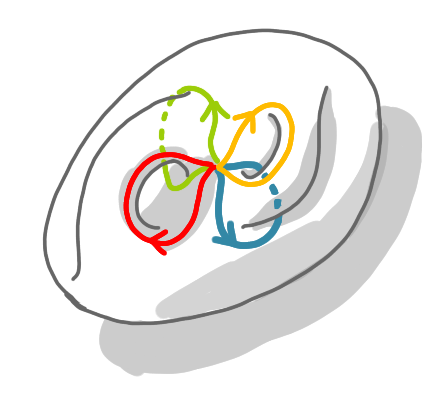
Nous avons maintenant deux poignées, et nous avons fini la construction. Pour rendre la figure plus lisible, tirons un peu sur la surface.
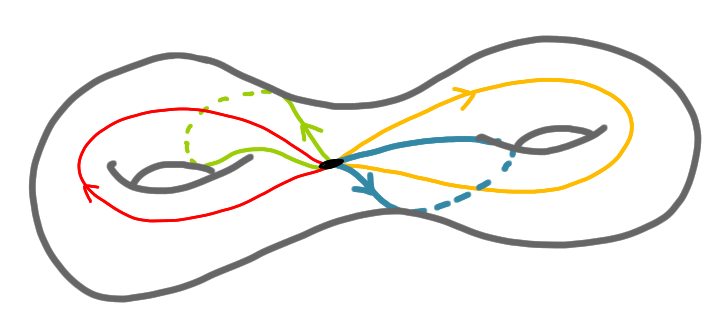
Une chose importante ici est que l’opération de collage est réversible. Pour revenir à l’octogone de départ, on peut simplement prendre des ciseaux et découper le long des quatre boucle.
Un théorème général (le théorème de classification des surfaces) établit que dans toute surface dites orientable, on peut trouver un ensemble de boucles tel que le découpage amène à un schéma polygonal. De plus, il existe un schéma polygonal canonique pour chaque surface. Plus le schéma est complexe, plus la surface est complexe. Les surfaces non-orientables, comme la bouteille de Klein peuvent être construites et caractérisées de manière similaire.
Pour en savoir plus, notamment sur les aspects algorithmiques, voir
ce document.