Un théorème de Gauss pour tenir une part de pizza

16 Feb 2021

J’ai laissé ce blog de coté pendant un moment. Voici une histoire de géométrie et de pizza, pour se remettre aux fourneaux. C’est aussi l’occasion d’essuyer les plâtres avec ma nouvelle tablette graphique. (Je referai les dessins plus tard, quand je l’aurai mieux en main.)

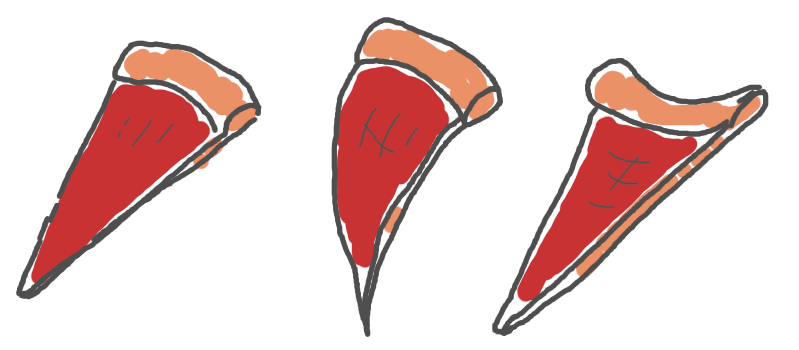
Une part de pizza dans plusieurs positions.

Un chouette article sur Images des maths fait le lien entre la technique qui consiste à plier une part de pizza pour qu’elle se tienne, et un théorème de courbure de Gauss. Je prends le thème à ma sauce.

Commençons par le théorème.

Theorème remarquable de Gauss (Theorema egregium): Deux surfaces de classe $C^3$ localement isométriques ont la même courbure de Gauss en tout point.

Deux choses pour commencer:

• $C^3$ est la notion standard de régularité : la troisième dérivée est continue partout.
• une isométrie locale est une transformation qui préserve les distances (sur la surface) au voisinage de chaque point. Par exemple prendre une surface plate et la coller sur un cylindre est une isométrie locale.

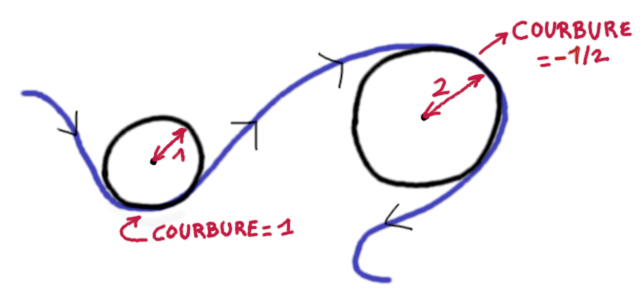
Passons à la notion de courbure de Gauss. D’abord, la courbure d’une courbe orientée se définit de façon naturelle avec le rayon $r$ d’un disque osculateur : $1/r$ si la courbe tourne à gauche et $-1/r$ si la courbe tourne à droite.

Ensuite pour une surface, on peut se ramener à une courbe en intersectant avec un plan. En fait on va se ramener à deux courbes, avec deux plans. Plus précisément, en tout point de la surface on peut définir un plan tangent, et l’on peut alors choisir deux autres plans, tels qu’ils soient tous les trois orthogonaux.

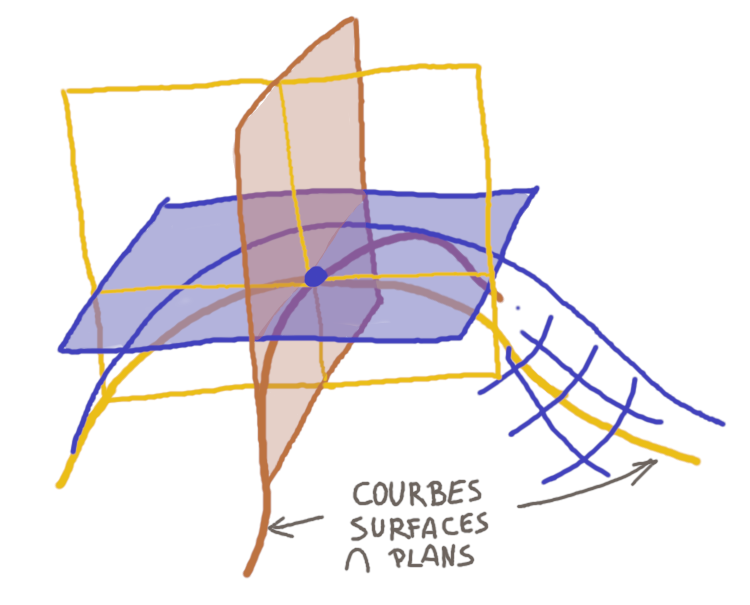
Ces deux plans définissent deux courbes, que l’on peut orienter de manière canonique. Il se trouve que si l’on fait tourner cette paire de plans intersectants, on arrive toujours à point où l’on a la courbure maximum sur l’un des plans et la courbure minimum sur l’autre. Ce sont les courbures principales. Sur mon premier dessin ce n’est pas très explicite, mais voilà un cas où l’on comprend bien ce qui se passe.

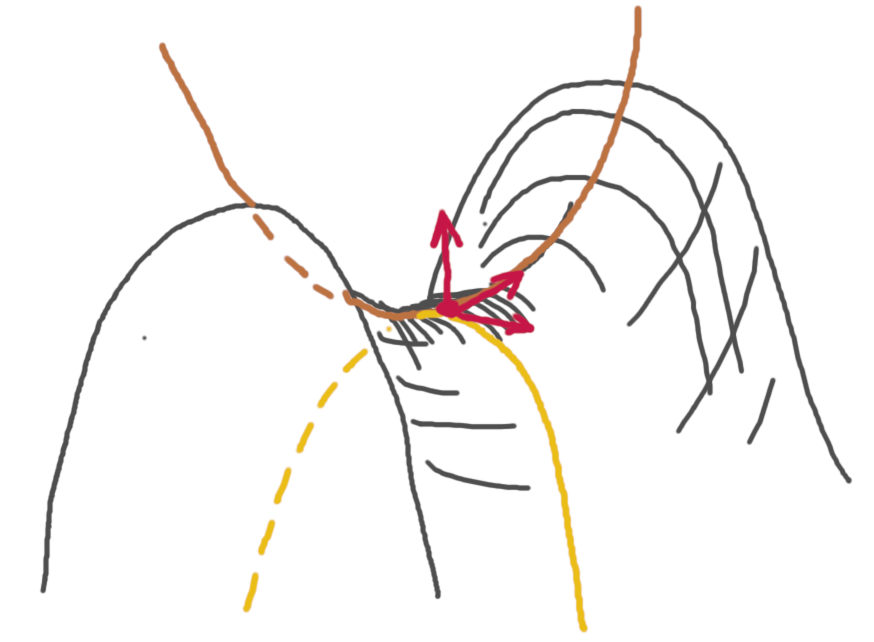
La courbure de Gauss en un point est le produit de ses courbures principales. Le signe de la courbure donne déjà une idée de la forme de la surface en ce point, comme sur l’image ci-dessous.

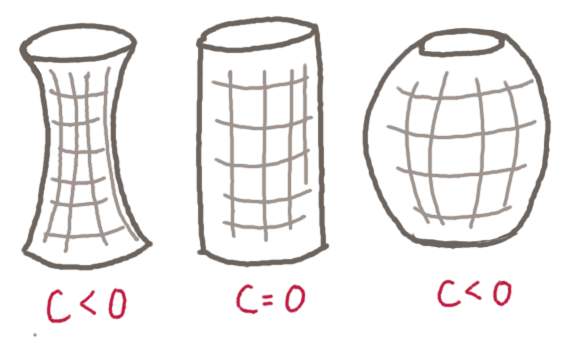
Maintenant que l’on a tous les ingrédients du théorème, il est temps de passer aux pizzas. Une part de pizza peut être posée à plat (comme à gauche dans la toute première image), sa courbure de Gauss est donc nulle en tout point, car les courbures principales sont nulles. Lorsque l’on plie la croûte de la pizza (comme à droite dans l’image), on fait une isométrie locale : la pizza n’est pas déchirée ou froissée et les sont conservées. La courbure doit donc rester nulle. La courbure maximum est celle qui est imprimée par la main, la courbure minimum est donc perpendiculaire. Et comme le produit doit être nul, cette dernière courbure doit être nulle, ce qui veut dire que la part de pizza ne va pas s’affaisser mais rester bien horizontale. Si on tient juste la pizza par la croute sans courber alors la courbure nulle peut être dans l’autre sens et la pizza s’affaissent (comme dans l’image du milieu)

Et on finit avec un dessert.